钦定四库全书
　缉古算经
　　　　　　　　　　　　唐　王孝通　撰
假令天正十一月朔夜半日在斗十度七百分度之四
百八十一章岁为母朔月行定分九千朔日定小馀一
万日法二万章岁七百亦名行分也今不取加时度问
天正朔夜半之时月在何处(推朔夜半月度旧术要须/加时日度自古先儒虽复)
(修撰改制意见甚众并未得算妙有理不尽考校尤难/臣每日夜思量常以此理屈滞恐后代无人知者今奉)

(敕造历因即改制为此新术旧推日度之术已得朔夜/半日度仍须更求加时日度然知月处臣今作新术但)
(得朔夜半日度不须加时日度即知月处此新术/比于旧术一年之中十二倍省功使学者易知)
　　　　荅曰在斗四度七百分度之五百三十
　　术曰(推朔夜半月度新术不复/加时日度月蚀乃可用之)以章岁减朔月行
　　定分馀以乘朔日定小馀满日法而一为先行分
　　不尽者半法已上收成一已下者弃之若先行分
　　满日行分而一为度分以减朔日夜半日所在度
　　分若度分不足减加往宿度其分不足减者退一

　　度为行分而减之馀即朔日夜半月行所在度及
　　分也(凡入历当月行定分即是月一日之行分但/此定分满章岁而一为度凡日一日行一度)
　　(然则章岁者即是日之一日行分也今按九章均/输篇有犬追兔术与此术相似彼问犬走一百步)
　　(兔走七十步令兔先走七十五步犬始追之问几/何步追及荅曰二百五十步追及彼术曰以兔走)
　　(减犬走馀者为法又以犬走乘兔先走为实实如/法而一即得追及步数此术亦然何者假令月行)
　　(定分九千章岁七百即是日行七百分月行九千/分令日月行数相减馀八千三百分者是日先行)
　　(之数然月始追之必用一日而相及也令定小馀/者亦是日月相及之日分假令定小馀一万即相)
　　(及定分此乃无对为数其日法者亦是相及之分/此又同数为有八千三百是先行分也斯则异矣)

　　(但用日法除之即四千一百五十即先行分故以/夜半之时日在月前月在日后以日月相去之数)
　　(四千一百五十减日行所在/度分即月夜半所在度分也)
假令太史造仰观台上广袤少下广袤多上下广差二
丈上下袤差四丈上广袤差三丈高多上广一十一丈
甲县差一千四百一十八人乙县差三千二百二十二
人夏程人功常积七十五尺限五日役台毕羡道从台
南面起上广多下广一丈二尺少袤一百四尺高多袤
四丈甲县一十三乡乙县四十三乡每乡别均赋常积

六千三百尺限一日役羡道毕二县差到人共造仰观
台二县乡人共造羡道皆从先给甲县以次与乙县台
自下基给高道自初登给袤问台道广高袤及县别给
高广袤各几何
　　　　荅曰
　　　　台高一十八丈
　　　　　上广七丈
　　　　　下广九丈

　　　　　上袤一十丈
　　　　　下袤一十四丈
　　　　甲县给高四丈五尺
　　　　　上广八丈五尺
　　　　　下广九丈
　　　　　上袤一十三丈
　　　　　下袤一十四丈
　　　　乙县给高一十三丈五尺

　　　　　上广七丈
　　　　　下广八丈五尺
　　　　　上袤一十丈
　　　　　下袤一十三丈
　　　　羡道高一十八丈
　　　　　上广三丈六尺
　　　　　下广二丈四尺
　　　　　袤一十四丈

　　　　甲县乡人给高九丈
　　　　　上广三丈
　　　　　下广二丈四尺
　　　　　上袤七丈
　　　　　下袤一十四丈
　　　　乙县乡人给高九丈
　　　　　上广三丈六尺
　　　　　下广三丈

　　　　　下袤七丈
　　术曰以程功尺数乘二县人又以限日乘之为台
　　积又以上下袤差乘上下广差三而一为隅阳羃
　　以乘截高为隅阳截积羃又半上下广差乘斩上
　　袤为隅头羃以乘截高为隅头截积所得并二积
　　以减台积馀为实以上下广差并上下袤差半之
　　为正数加截上袤以乘截高所得增隅阳羃加隅
　　头羃为方法又并截高及截上袤与正数为廉法

　　从闻立方除之即得上广各加差得台下广及上
　　下袤高
　　求均给积尺受广袤术曰以程功尺数乘乙县人
　　又以限日乘之为乙积三因之又以高羃乘之以
　　上下广差乘袤差而一为实又以台高乘上广广
　　差而一为上广之高又以台高乘上袤差而一为
　　上袤之高又以上广之高乘上袤之高三之为方
　　法又并两高三之二而一为廉法从开立方除之

　　即乙高以减本高馀即甲高此是从下给台甲高
　　又以广差乘乙高以本高而一所得加上广即甲
　　上广又以袤差乘乙高如本高而一所得加上袤
　　即甲上袤其甲上广袤即乙下广袤台上广袤即
　　乙上广袤其后求广袤有增损者皆放此(此应三/因乙积)
　　(台高冉乘上下广差冉乘袤差而一又以台高乘/上广为上广之高又以台高乘上袤为上袤之高)
　　(为小羃二因下袤之高为中羃一凡下袤下广之/高即是截高与上袤与上广之高相连并数然此)
　　(有中羃定有小羃一又有上广之高乘截高为羃之/各一又下广之高乘下袤之高为大羃二乘上袤)

　　(高为中羃一其大羃之中又小羃一复有上广上/袤之高为中羃各乘截高为中羃各一又截高自)
　　(乘为羃一其中羃之内有小羃一又上袤之高乘/截高为羃一然则截高自相乘为羃二小羃六又)
　　(上广上袤之高各三以乘截高为羃六令皆半之/故以三乘小羃又上广上袤之高各三令但半之)
　　(各得一又二分之一故三/之二而一诸羃截为积尺)
　　求羡道广袤高术曰以均赋常积乘二县五十六
　　乡又六因为积又以道上广多下广数加上广少
　　袤为下广少袤又以高多袤加下广少袤为下广
　　少高以乘下广少袤为隅阳羃又以下广少上广

　　乘之为鳖隅以减积馀三而一为实并下广少袤
　　与下广少高以下广少上广乘之为鳖从横廉羃
　　三而一加隅羃为方法又以三除上广多下广以
　　下广少袤下广少高加之为廉法从开立方除之
　　即下广加广差即上广加袤多上广于上广即袤
　　加广多袤即道高
　　求羡道均给积尺甲县受广袤术曰以均赋常积
　　乘甲县一十三乡又六因为积以袤再乘之以道

　　上下广差乘台高为法而一为实又三因下广以
　　袤乘之如上下广差而一为都廉从开立方除之
　　即甲袤以广差乘甲袤本袤而一以下广加之即
　　甲上广又以台高乘甲袤本袤除之即甲高
假令筑堤西头上下广差六丈八尺二寸东头上下广
差六尺二寸东头高少于西头高三丈一尺上广多东
头高四尺九寸正袤多于东头高四百七十六尺九寸
甲县六千七百二十四人乙县一万六千六百七十七

人丙县一万九千四百四十八人丁县一万二千七百
八十一人四县每人一日穿土九石九斗二升每人一
日筑常积一十一尺四寸十三分寸之六穿方一尺得
土八斗古人负土二斗四升八合平道行一百九十二
步一日六十二到今隔山渡水取土其平道只有一十
一步山斜高三十步水宽一十二步上山三当四下山
六当五水行一当二平道踟蹰十加一载输一十四步
减计一人作功为均积四县共造一日役毕今从东头

与甲其次与乙丙丁问给斜正袤与高及下广并每人
一日自穿运筑程功及堤上下高广各几何
　　　　荅曰
　　　　一人一日自穿运筑程功四尺九寸二分
　　　　西头高三丈四尺一寸
　　　　　上广八尺
　　　　　下广七丈六尺二寸
　　　　东头高三尺一寸

　　　　　上广八尺
　　　　　下广一丈四尺二寸
　　　　　正袤四十八丈
　　　　　斜袤四十八丈一尺
　　　　甲县正袤一十九丈二尺
　　　　　斜袤一十九丈二尺四寸
　　　　　下广三丈九尺
　　　　　高一丈五尺五寸

　　　　乙县正袤一十四丈四尺
　　　　　斜袤一十四丈四尺三寸
　　　　　下广五丈七尺六寸
　　　　　高二丈四尺八寸
　　　　丙县正袤九丈六尺
　　　　　斜袤九丈六尺二寸
　　　　　下广七尺
　　　　　高三丈一尺

　　　　丁县正袤四丈八尺
　　　　　斜袤四丈八尺一寸
　　　　　下广七丈六尺二寸
　　　　　高三丈四尺一寸
　　求人到程功运筑积尺术曰置上山四十步下山
　　二十五步渡水二十四步平道一十一步踟蹰之
　　间十加一载输一十四步一返计一百二十四步
　　以古人负土二斗四升八合平道行一百九十二

　　步以乘一日六十二到为实却以一返步为法除
　　得自运土到数也又以一到负土数乘之却以穿
　　方一尺土数除之得一人一日运功积又以一人
　　穿土九石九斗二升以穿方一尺土数除之为法
　　除之得穿用人数复置运功积以每人一日常积
　　除之得筑用人数并之得六人共成二十九尺七
　　寸六分以六人除之即一人程功也
　　求堤上下广及高袤术曰一人一日程功乘总人

　　为堤积以高差乘下广差六而一为鳖羃又以高
　　差小头广差二而一为大卧堑头羃又半高差乘
　　上广多东头高之数为小卧堑头羃并三羃为大
　　小堑鳖率乘正袤多小高之数以减堤积馀为实
　　又置半高差及半小头广差与上广多小头高之
　　数并三差以乘正袤多小头高之数以加率为方
　　法又并正袤多小头并上广多小高及半高差而
　　增之兼半小头广差加之为廉法从开方立除之

　　即小高加差即各得广袤高又正袤自乘高差自
　　乘并而开方除之即斜袤
　　求甲县高广正斜袤术曰以程功乘甲县人以六
　　因取积又乘袤羃以下广差乘高差以法除之为
　　实又并小头上下广以乘小高三因之为垣头羃
　　又乘袤羃如法而一为垣方又三因小头下广以
　　乘正袤以广差除之为都廉从开立方除之得小
　　头即甲袤又以下广差乘之所得以正袤除之所

　　得加东头下广即甲广又以两头高差乘甲袤以
　　正袤除之以加东头高即甲高又以甲袤自乘以
　　堤东头高减甲高馀自乘并二位以开方除之即
　　得斜袤求高广以本袤及高广差求之若求乙丙
　　丁各以本县人功积尺每以前大高广为后小高
　　广凡廉母自乘为方母廉母乘方母为实母(此平/堤在)
　　(上羡除在下两高之差即除高其馀两边各一鳖/腝中一堑堵今以袤再乘积广差乘袤差而一得)
　　(截鳖腝袤再乘为立方一又堑堵袤自乘为羃三/又三因小头下广大袤乘之广差而一与羃为高)

　　(故为廉法又并小头上下广又三之意同六除然/此头羃本乘截袤又袤乘之差相乘而一今还依)
　　(数乘除一头羃为/从得截袤为广)
　　求堤都积术曰置西头高倍之加东头高又并西
　　头上下广半而乘之又置东头高倍之加西头高
　　又并东头上下广半而乘之并二位积以正袤乘
　　之六而一得堤积也
假令筑龙尾堤其堤从头高上阔以次低狭至尾上广
多下广少堤头上下广差六尺下广少高一丈二尺少

袤四丈八尺甲县二千三百七十五人乙县二千三百
七十八人丙县五千二百四十七人各人程功常积一
尺九寸八分一日役毕三县共筑今从堤尾与甲县以
次与乙丙问龙尾堤从头至尾高袤广及各县别给高
袤广各多少
　　　　荅曰
　　　　　高三丈
　　　　　上广二丈四尺

　　　　　下广一丈八尺
　　　　　袤六丈六尺
　　　　甲县高一丈五尺
　　　　　袤三丈三尺
　　　　　上广二丈一尺
　　　　乙县高二丈一尺
　　　　　袤一丈三尺二寸
　　　　　上广二丈二尺二寸

　　　　丙县高三丈
　　　　　袤一丈九尺八寸
　　　　　上广二丈四尺
　　求龙尾堤广袤高术曰以程功乘总人为堤积又
　　六因之为虚积以少高乘少袤为隅羃以少上广
　　乘之为鳖隅羃以减虚积馀三约之所得为实并
　　少高袤以少上广乘之为鳖从横廉羃三而一加
　　隅羃为方法又三除少上广以少袤少高加之为

　　廉法从开立方除之得下广加差即高广袤
　　求逐县均给积尺受广袤术曰以程功乘当县人
　　为积尺各六因积尺又乘袤羃广差乘高为法除
　　之为实又三因末广以袤乘之广差而一为都廉
　　从开立方除之即甲袤以本高乘之以本袤除之
　　即甲高又以广差乘甲袤以本袤除之所得加末
　　广即甲上广其甲上广即乙末广其甲高即垣高
　　求都廉如前又并甲上下广三之乘甲高以乘袤

　　羃以法除之得垣方从开立方除之即乙袤馀放
　　此(此龙尾犹羡除也其堑堵一鳖腝一并而相连/今以袤再乘积广差乘高而一所得截鳖腝袤)
　　(再自乘为立方一又各一鳖腝截袤再自乘为立/方一又堑堵袤自乘为羃三又三因末广以袤乘)
　　(之广差而一与羃/为高故为廉法)
假令穿河袤一里二百七十六步下广六步一尺二寸
北头深一丈八尺六寸上广十二步二尺四寸南头深
二百四十一尺八寸上广八十六步四尺八寸运土于
河西岸造漘北头高二百二十三尺二寸南头无高下

广四百六尺七寸五氂袤与河同甲郡二万二千三百
二十人乙郡六万八千七十六人丙郡五万九千九百
八十五人丁郡三万七千九百四十四人自穿负筑各
人程功常积三尺七寸二分限九十六日役河漘俱了
四郡分共造漘其河自北头先给甲郡以次与乙合均
赋积尺问逐郡各给斜正袤上广及深并漘上广各多
少
　　　　荅曰

　　　　漘上广五丈八尺二寸一分
　　　　甲郡正袤一百四十四丈
　　　　　斜袤一百四十四丈三尺
　　　　　上广二十六丈四寸
　　　　　深一十一丈一尺六寸
　　　　乙郡正袤一百一十五丈二尺
　　　　　斜袤一百一十五丈四尺四寸
　　　　　上广四十丈九尺二寸

　　　　　深一十八丈六尺
　　　　丙郡正袤五十七丈六尺
　　　　　斜袤五十七丈七尺二寸
　　　　　上广四十八丈三尺六寸
　　　　　深二十二丈三尺二寸
　　　　丁郡正袤二十八丈八尺六寸
　　　　　斜袤二十八丈八尺六寸
　　　　　上广五十二丈八寸

　　　　　深二十四丈一尺八寸
　　术曰如筑堤术入之(覆堤为河彼注甚明高深/稍殊程功是同意可知也)以
　　程功乘甲郡人又以堤日乘之四之三而一为积
　　又六因以乘袤羃以上广差乘深差为法除之为
　　实又并小头上下广以乘小头深三之为垣头羃
　　又乘袤羃以法除之为垣方三因小头上广以乘
　　正袤以广差除之为都廉从开立方除之即得小
　　头为甲袤求深广以本袤及深广差求之为法以

　　两头上广差乘甲袤以本袤除之所得加小头上
　　广即甲上广以小头深减南头深馀以乘甲袤以
　　本袤除之所得加小头深即甲深又正袤自乘深
　　差自乘并而开方除之即斜袤若求乙丙丁每以
　　前大深广为后小深广准甲求之即得
　　求漘上广术曰以程功乘总人又以限日乘之为
　　积六因之为实以正袤除之又以高除之所得以
　　下广减之馀又半之即漘上广

假令四郡输粟斛法二尺五寸一人作功为均自上给
甲以次与乙其甲郡输粟三万八千七百四十五石六
斗乙郡输粟三万四千九百五石六斗丙郡输粟二万
六千二百七十石四斗丁郡输粟一万四千七十八石
四斗四郡共穿窖上袤多于上广一丈少于下袤三丈
多于深六丈少于下广一丈各计粟多少均出丁夫自
穿负筑冬程人功常积一十二尺一日役问窖上下广
袤深郡别出人及窖深广各多少

　　　　荅曰
　　　　窖上广八丈
　　　　　上袤九丈
　　　　　下广一十丈
　　　　　下袤一十二丈
　　　　　深三丈
　　　　甲郡八千七十二人
　　　　　深一十二尺

　　　　　下袤一十丈二尺
　　　　　广八丈八尺
　　　　乙郡七千二百七十二人
　　　　　深九尺
　　　　　下袤一十一丈一尺
　　　　　广九丈四尺
　　　　丙郡五千四百七十三人
　　　　　深六尺

　　　　　下袤一十一丈七尺
　　　　　广九丈八尺
　　　　丁郡二千九百三十三人
　　　　　深三尺
　　　　　下袤一十二丈
　　　　　广一十丈
　　求窖深广袤术曰以斛法乘总粟为积尺又广差
　　乘袤差三而一为隅阳羃乃置堑上广半广差加

　　之以乘堑上袤为隅阳羃及隅头羃加之为方法
　　又置堑上袤及堑上广并之为大广又并广差及
　　袤差半之以加大广为廉法从开立方除之即深
　　各加差即合所问
　　求均给积尺受广袤深术曰如筑堤术入之以斛
　　法乘甲郡输粟为积尺又三因以深羃乘之以广
　　差乘袤差而一为实深乘上广广差而一为上广
　　之高深乘上袤袤差而一为上袤之高上广之高

　　乘上袤之高三之为方法又并两高三之二而一
　　为廉法从开立方除之即甲深以袤差乘之以本
　　深除之所得加上袤即甲下袤以广差乘之本深
　　除之所得加广即甲下广若求乙丙丁每以前下
　　广袤为后上广袤以次皆准此求之即得若求人
　　数各以程功约当郡积尺
假令亭仓上小下大上下方差六尺高多上方九尺容
粟一百八十七石二斗今已运出五十石四斗问仓上

下方高及馀粟深上方各多少
　　　　荅曰
　　　　　上方三尺
　　　　　下方九尺
　　　　　高一丈二尺
　　　　　馀粟深上方俱六尺
　　求仓方高术曰以斛法乘容粟为积尺又方差自
　　乘三而一为隅阳羃以乘截高以减积馀为实又

　　方差乘截高加隅阳羃为方法又置方差加截高
　　为廉法从开立方除之即上方加差即合所问
　　求馀粟高及上方术曰以斛法乘出粟三之以乘
　　高羃令方差羃而一为实(此是大小高各自乘又/相乘各乘取高是大高)
　　(者即是取高/与小高并)高乘上方方差而一为小高令自乘
　　三之为方法三因小高为廉法从开立方除之得
　　取出高以减本高馀即残粟高置出粟高又以方
　　差乘之以本高除之所得加上方即馀粟上方(此/本)

　　(术曰上下方相乘又各自乘并以高乘之三而一/今还元三之又高羃乘之差羃而一得大小高相)
　　(乘又各自乘之数何者若高乘下方方差而一得/大高也若高乘上方方差而一得小高也然则斯)
　　(本下方自乘故须高自乘乘之差自乘而一即得/大高自乘之数小高亦然凡大高者即是取高与)
　　(小高并相连今大高自乘为大方大方之内即有/取高自乘羃一隅头小高自乘羃一又其两边各)
　　(一以取高乘小高为羃二又大小高相乘为中方/中方之内即有小高乘取高羃一又小高自乘即)
　　(是小方之羃又一则小高乘大高又各自乘三等/羃皆以乘取高为立积故三因小羃为方及三小)
　　(高为/廉也)
假令刍甍上袤三丈下袤九丈广六丈高一十二丈有

甲县六百三十二人乙县二百四十三人夏程人功当
积三十六尺限八日役自穿筑二县共造今甲县先到
问自下给高广袤各多少
　　　　荅曰
　　　　　高四丈八尺
　　　　　上广三丈六尺
　　　　　袤六丈六尺
　　求甲县均给积尺受广袤术曰以程功乘乙县人

　　数又以限日乘之为积尺以六因之又高羃乘之
　　又袤差乘广而一所得又半之为实高乘上袤袤
　　差而一为上袤之高三因上袤之高半之为廉法
　　从开立方除之得乙高以减甍高馀即甲高求广
　　袤依率求之(此乙积本倍下袤上袤从之以下广/及高乘之六而一为一甍积今还元)
　　(须六因之以高羃乘之为实袤差乘广而一得取/高自乘以乘二上袤之高并大广袤相连之数则)
　　(三小高为廉法各以取高为方仍有取高/为立方者故半之为立方一又须半廉法)
假令圆囤上小下大斛法二尺五寸以率径一周三上

下周差一丈二尺高多上周一丈八尺容粟七百五斛
六斗今已运出二百六十六石四斗问残粟去口上下
周高各多少
　　　　荅曰
　　　　上周一丈八尺
　　　　下周三丈
　　　　高三丈六尺
　　　　去口一丈八尺

　　　　粟周二丈四尺
　　求圆囤上下周及高术曰以斛法乘容粟又三十
　　六乘之三而一为方亭之积又以周差自乘三而
　　一为隅阳羃以乘截高以减亭积馀为实又周差
　　乘截高加隅阳羃为方法又以周差加截高为廉
　　法从开立方除之得上周加差而合所问
　　求粟去口术曰以斛法乘出斛三十六乘之以乘
　　高羃如周差羃而一为实高乘上周周差而一为

　　小高令自乘三之为方法三因小高为廉法从开
　　立方除之即去口(三十六乘讫即是截/方亭之前方窖不别)置去口以
　　周差乘之以本高除之所得加上周即粟周
假令有粟二万三千一百二十斛七斗三升欲作方仓
一圆窖一盛各满中而粟适尽令高深等使方面少于
圆径九寸多于高二丈九尺八寸率径七周二十二问
方径深多少
　　　　荅曰

　　　　仓方四丈五尺三寸(容粟一万二千七百二/十二斛九斗五升八合)
　　　　窖径四丈六尺二寸(容粟一万三百九十/七石七斗七升二合)
　　　　高与深各一丈五尺五寸
　　求方径高深术曰十四乘斛法以乘粟数二十五
　　而一为实又倍多加少以乘少数又十一乘之二
　　十五而一多自乘加之为方法又倍少数十一乘
　　之二十五而一又倍多加之为廉法从开立方除
　　之即高深各加差即方径(一十四乘斛法以乘粟/为积尺前一十四除今)

　　(还元一十四乘为径自乘者是一十一方自乘者/是一十四故并之为二十五凡此方圆二径长短)
　　(不同二径各自乘为方大小各别然则此堑方二/丈九尺八寸堑径三丈七寸皆成立方此应堑方)
　　(自乘一十四乘之堑径一十一乘之二十五而一/为隅羃即方法也但二隅皆以堑数为方面今此)
　　(术就省倍小隅方加差为短以差乘之为短羃一/十一乘之二十五而一又小隅方自乘之数即是)
　　(方圆之隅同有此此数若二十五乘之还须二十/五除直以小隅方自乘加之故不复乘除又须倍)
　　(二廉之差一十一乘之二十五而一倍二/廉加之故为廉法不复二十五乘除之也)
　　还元术曰仓方自乘以高乘之为实圆径自乘以
　　深乘之一十一乘一十四而一为实皆以斛法除

　　之即得容粟(斛法二/尺五寸)
假令有粟一万六千三百四十八石八斗欲作方仓四
圆窖三令高深等方面少于圆径一丈多于高五尺斛
法二尺五寸率径七周二十二问方高径多少
　　　　荅曰
　　　　方一丈八尺
　　　　高深一丈三尺
　　　　圆径二丈八尺

　　术曰以一十四乘斛法以乘粟数如八十九而一
　　为实倍多加少以乘少数三十三乘之八十九而
　　一多自乘加之为方法又倍少数以三十三乘之
　　八十九而一倍多加之为廉法从开立方除之即
　　高深各加差即方径(一十四乘斛法以乘粟为径/自乘及方自乘数与前同今)
　　(方仓四即四因十四圆窖三即三因十一并之为/八十九而一此堑径一丈五尺堑方五尺以高为)
　　(立方自外/意同前)
假令有粟三千七十二石欲作方仓一圆窖一令径与

方等方多于窖深二尺少于仓高三尺盛各满中而粟
适尽(圆率斛法/并与前同)问方径高深各多少
　　　　荅曰
　　　　方径各一丈六尺
　　　　高一丈九尺
　　　　深一丈四尺
　　术曰三十五乘粟二十五而一为率多自乘以并
　　多少乘之以乘一十四如二十五而一所得以减

　　率馀为实并多少以乘多倍之乘一十四如二十
　　五而一多自乘加之为方法又并多少以乘一十
　　四如二十五而一加多加之为廉法从开立方除
　　之即窖深各加差即方径高(截高五尺堑径及方/二尺以深为立方十)
　　(四乘斛法故三十五乘粟多自乘并多少乘之为/截高隅积减率馀即二方廉各二尺长五尺自外)
　　(意旨皆/与前同)
假令有粟五千一百四十五石欲作方窖圆窖各一令
口小底大方面于圆径等两深亦同其深少于下方七

尺多于上方一丈四尺盛各满中而粟适尽(圆率斛法/并与前同)
问方径深各多少
　　　　荅曰
　　　　上方径各七尺
　　　　下方径各二丈八寸
　　　　深各二丈一尺
　　术曰以四十二乘斛法以乘粟七十五而一为方
　　亭积令方差自乘三而一为隅阳羃以截多乘之

　　减积馀为实以多乘差加羃为方法多加差为廉
　　法从开立方除之即上方加差即合所问(凡方亭/上下方)
　　(相乘又命自乘并以乘高为虚命三而一为方亭/积若圆亭上下径相乘又各自乘并以乘高为虚)
　　(又十一乘之四十二而一为圆亭积今方圆二积/并在一处故以四十二复乘之即得圆虚十一方)
　　(虚十四凡二十五而一得一虚之积又三除虚积/为方亭实乃依方高覆问法见上下方差及高差)
　　(与积求上下方高术入/之故三乘二十五而一)
假令有粟二万六千三百四十二石四斗欲作方窖六
圆窖四令口小底大方面与圆径等其深亦同令深少

于下方七尺多于上方一丈四尺盛各满中而粟适尽
(圆率斛法/并与前同)问上下方深数各多少
　　　　荅曰
　　　　方窖上方七尺
　　　　下方二丈八尺
　　　　深二丈一尺
　　　　圆窖上下方深与方窖同
　　术曰以四十二乘斛法以乘粟三百八十四而一

　　为方亭积尺令方差自乘三而一为隅阳羃以截
　　多乘之以减积馀为实以多乘差加羃为方法又
　　以多加差为廉法从开立方除之即上方加差即
　　合所问(今以四十二乘圆虚十一者四方虚十四/者六合一百二十八虚除之为一虚之积)
　　(得者仍三而一为方亭实积乃依方亭见/差覆问求之故三乘一百二十八除之)
假令有句股相乘羃七百六五十分之一弦多于句三
十六十分之九问三事各多少
　　　　荅曰

　　　　句十四二十分之七
　　　　股四十九五分之一
　　　　弦五十一四分之一
　　术曰羃自乘倍多数而一为实半多数为廉法从
　　开立方除之即句以弦多句加之即弦以句除羃
　　即股(句股相乘羃自乘与句羃乘股羃积等故以/倍句弦差而一得一句与半差之共乘句羃)
　　(为方故半差为廉从开立方除之三按此/术原本不全今依句股义拟补十 字)
假令有句股相乘羃四千三十六五分之○股少于弦

六五分之一问弦多少(按此问原本缺二字今依文补/一股字其股字上之○系所设)
(分数未便悬/拟今姑阙之)
　　　　荅曰弦一百一十四十分之七
　　术曰羃自乘倍少数而一为实半少为廉法从开
　　立方除之即股加差即弦
假令有句弦相乘羃一千三百三十七二十分之一弦
多股一十分之一问股多少
　　　　荅曰九十二五分之二

　　术曰羃自乘倍多而一为立羃又多再　乘半之
　　减立羃馀为实又多数自乘　　为方法又置多
　　数五之二而一为廉　　开立方除之即股(句弦/相乘)
　　(羃自股与半羃乘弦羃之/得一 差)　(为方令股弦差而一/ 多再自乘半)
　　(之为隅/)　　(倍之为横虚二立廉/ 从隅)
　　(故五多为上广即二多术原本不全今加案于法/ 之二而一○案此 后)
　　(并别立一术绘图/加说以补其阙)
　　　案此术脱简既多法亦烦扰宜云羃自乘多数

　　　而一所得四之为实多为廉法从立方开之得
　　　减差半之即股(羃自乘与勾羃弦羃相乘积等令/勾羃变为股弦并乘股弦差故差)
　　　(而一所得乃股/弦并乘弦羃)

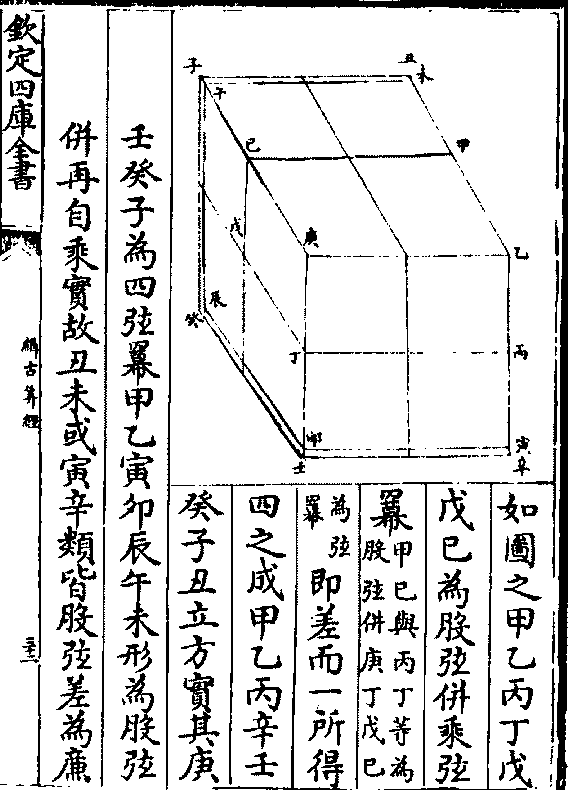　　　　　　　　　　　　　如图之甲乙丙丁戊
　　　　　　　　　　　　　戊巳为股弦并乘弦
　　　　　　　　　　　　　羃(甲巳与丙丁䓁为/股弦并庚丁戊巳)
　　　　　　　　　　　　　(为弦/羃)即差而一所得
　　　　　　　　　　　　　四之成甲乙丙辛壬
　　　　　　　　　　　　　癸子丑立方实其庚
　　　壬癸子为四弦羃甲乙寅卯辰午未形为股弦
　　　并再自乘实故丑未或寅辛类皆股弦差为廉

　　　实之从开得甲己类股弦并减差半之得股矣
假令有股弦相乘羃
三句少于弦五十
　　　　荅曰六
　　术曰羃自乘
　　再自乘半之以矣
　　乘倍之为方法
　　廉法从开立方

　　羃即股
假令有股弦相乘羃
七问股多少
　　　　荅曰股二十
　　术曰羃自
　　除之所得
　　(数亦是股/为长以股)
　　(得股羃又开/股北分母常)

假令有股十六二分
十四二十五分
　　　　荅曰
　　术曰羃自乘
　　除之所得又开方
　
　
　缉古算经